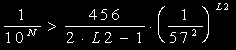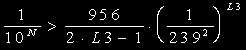
4.ストーマーの公式によるπの計算方法
(1)公式の展開
・それではいよいよ計算の仕方を考えてみます。
まずはストーマーの公式を具体的に記述します。
第1第2及び第3項を級数展開すると下式のようになります。
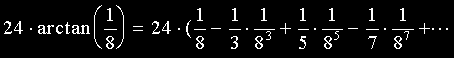
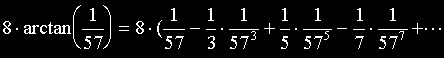
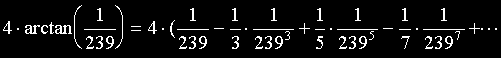 さらに、後で計算しやすいように、少し変形します。それと第n項もきちんと書いておきます。
さらに、後で計算しやすいように、少し変形します。それと第n項もきちんと書いておきます。
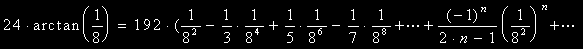 ------(A)
------(A)
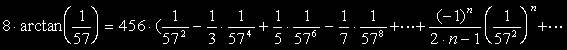 -------(B)
-------(B)
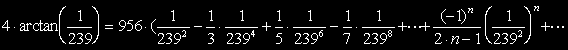 -------(C)
これらの級数の各項を必要な桁数計算し,最後に加算するとπが求まるわけです。
-------(C)
これらの級数の各項を必要な桁数計算し,最後に加算するとπが求まるわけです。
(2)計算精度の決め方
・たとえば、小数点以下N桁計算するなら,(A)に着目して、不等式
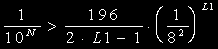 を満たすL1番目の項以降は,計算する必要は無いわけです。
を満たすL1番目の項以降は,計算する必要は無いわけです。
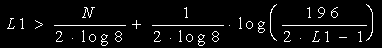 で、この式を変形して, この不等式を満たす最小のL1を求めれば良いわけです。
で、この式を変形して, この不等式を満たす最小のL1を求めれば良いわけです。
右辺を眺めると,第2項は単調減少することは明らかです。L1=1の時最大で,1.27です。L1=2では,1.00
L1=3 以降では1未満になります。つまり,項数を計算する上で,右辺第2項の部分はせいぜい2しか寄与しないのです。
従ってL1は下式で計算し、結果に2を加算すれば十分でしょう。
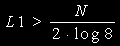 ・これと同様に(B)についても調べてみましょう。
・これと同様に(B)についても調べてみましょう。
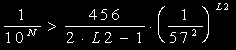 ですから、
ですから、
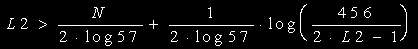 となって,右辺第2項は,L2=1で0.757であり,最初から1未満です。従って,(B)については下式より必要な項数L2を
求めることができます。
となって,右辺第2項は,L2=1で0.757であり,最初から1未満です。従って,(B)については下式より必要な項数L2を
求めることができます。
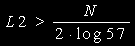 ・最後に(C)です。
・最後に(C)です。
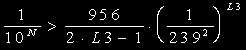
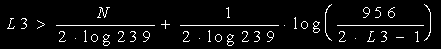 右辺第2項は,L3=1では0.626であり,②’同様1未満の寄与しかしません。
L3は下式から計算すれば十分です。
右辺第2項は,L3=1では0.626であり,②’同様1未満の寄与しかしません。
L3は下式から計算すれば十分です。
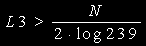 これらからから,円周率の桁数に対して必要な項数を計算し,これを下の表にまとめておきます。上の説明の通り,2程度の寄与は有りますので,下表では2を加算してます。
これらからから,円周率の桁数に対して必要な項数を計算し,これを下の表にまとめておきます。上の説明の通り,2程度の寄与は有りますので,下表では2を加算してます。
表1 計算に必要な項数
| 計算桁数 |
(A) |
(B) |
(C) |
| 100 |
57 |
30 |
23 |
| 1,000 |
555 |
286 |
212 |
| 10,000 |
5,533 |
2,849 |
2,104 |
| >100,000< |
55,367 |
28,477 |
21,024 |
| 1,000,000 |
553,656 |
284,760 |
210,227 |



![]()
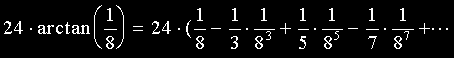
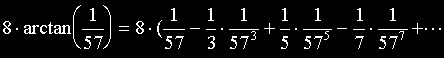
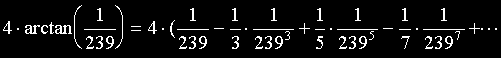
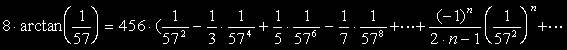 -------(B)
-------(B)
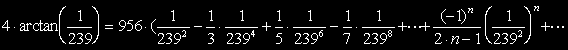 -------(C)
-------(C)