宇宙

6.計算方法の工夫

（１）性能比較


さて，無事プログラムが動くようになりました。まともに動くようになると， 今度は速くしたいと言う欲が出てきます。この章ではどうやって速くできるのかを説明します。 あらかじめお断りしますが，速くする方法はここで説明する方法だけではありません。一例です。

(1)性能比較
下表に各桁を計算させた時の時間を示します。
実行環境
CPU Pentium 100
Windows95 のDOSプロンプト
LSI C-86 Ver 3.30 試食版

これは，計算開始と終了時に _dos_gettime()（システム時刻の取得関数）を実行して得たシステム時間の差です。 桁数が2倍になると，時間はほぼ4倍になるのが分かると思います。最初に挙げたガウスやマーチンの公式も同様です。 測定値がどこまで正確か、というのは大いに疑問ですが、相対的な比較に使えるかと思います。

下段はこの章で説明する工夫をした結果です。2000桁のところで比較すると，所用時間は36％余り削減， つまり約1.5倍ほど高速化と言うことになります。
表6-１性能（単位 秒）
計算桁数 400 500 800 1000 2000 3000
対策前 0.27 0.33 0.88 1.21 4.62 10.44
対策後 0.11 0.16 0.49 0.77 2.97 6.67



（２）除算の削減

4章での(A)(B)(C)を見ていただければ分かりますが，共通している部分があります。それは2n-1による除算です。
計算の手順としては，(A)の計算がすべて終わってから(B)へと進みますから，2n-1による除算は3回実行することになります。 これを回避するには，(A)(B)(C)を並行に計算すれば良いわけです。
最初の2項は下記のようになります。



並行に計算するにしても， (A)(B)(C)では計算する項数が異なりますから，2n-1での除算が3分の1になるわけではありません。 例えば，1000の場合は，555 + 286 + 212 =1053 回2n-1で除算します。さらに2n-1 1回の除算には配列要素の数だけ繰り返しがありますから，1053×配列要素数 回となるのですが，簡単のため配列要素数を無視します。すると，
表6-2 除算の削減
項番 対象となる級数 削減回数
1-212 (A)、(B)、(C) 212 * 2 = 424
213-286 (A)、(B) 73
287-555 (A) 0


合計で517回削減できます。これは，全体の半分に相当します。 と言っても，57や239と言う分母の除算はまったく削減できていませんから，2倍の速さになるわけではありません。
その結果は，(1)で説明したとおりです。


(3)0の無視

82，572，2392での除算は，計算が進むと大きさが急速に小さくなります。 その結果，配列要素のかなりの部分は0になるはずです。0に対して計算を行うのはまったく無駄ですから， これを削減します。

級数(A)に着目して，


これから、Ｌとxを具体的に計算してみましょう。
表6-3
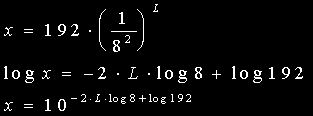
L -2Llog8 -2Llog8 + log192 x
1 -1.806 0.477 2.999
2 -3.612 -1.323 0.0475 33
3 -5.418 -3.135 0.0007 3282 4
4 -7.224 -4.941 0.0000 1145 5
5 -9.030 -6.747 0.0000 0017 9


[]を内部の数値を超えない最大の整数を表すとすると，[2Llog8-log192]+1 桁目に、0でない数値が現れることが分かります。つまり以上のことから，82での除算では，[2Llog8-log192]+1 桁目以降の配列を対象に計算を行えば無駄が省けます。

他の項も同様ですが、なかなか難しいです。


級数(B)に着目して，
表6-4
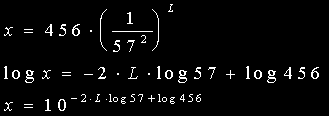
L -2Llog57 -2Llog57 + log456 x
1 -3.511 -0.8520 0.1406
2 -7.022 -4.3630 0.0000 4335
3 -10.535 -7.8760 0.0000 0001 3
4 -14.047 -11.388 0.0000 0000 0004 09
5 -17.559 -14.900 0.0000 0000 0000 0012


[2 L2 log57-log456]+1桁目に初めて0でない数字が現れます。

級数(B)に着目して，
表6-5
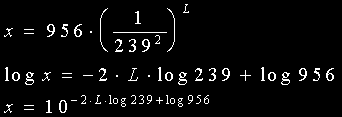
L -2Llog239 -2Llog239 + log956 x
1 -4.756 -1.776 0.0167
2 -9.5136 -6.533 0.0000 0029 3
3 -14.270 -11.290 0.0000 0000 0005 12
4 -19.027 -16.047 0.0000 0000 0000 0000 897
5 -23.784 -20.804 0.0000 0000 0000 0000 000

[2 L3 log239-log956]+1桁目に0でない数値が現れていることがわかります。


・次に，0で無い桁が収まる最初の配列要素がどれかを調べます。
10000進法を採用しているので，1つの配列要素には4桁の数値が収まります。従って，

4(k-1)+1 <= [2Llog8-log192]+1 <= 4k （ここで， k=1,2,3,4,･･･とする）

を満たすkを求めれば良いわけです。例えば，L=5 ならば，表6-3より，7となりますから，

4(k-1)+1 <= 7 <= 4k
ゆえに k = 2

つまり，配列要素の2番目から計算を始めれば良いわけです。一般には，下式で計算できます。




ただし，この手法では級数の新しい項を計算する前に毎回このチェック処理を行わなければなりません。従って，計算桁数が小さい場合は却って性能が下がりそうです。

目次へ戻る
宇宙