RGB、CMYの不思議
光の三原色を全て集めると白くなり、絵の具の三原色は黒くなるのだと学校で教わったときには、なにか納得できないような気持のまま、光は透き徹っているから白で、絵の具は濁っているから黒くなるのだと勝手な解釈をしていました。こういった解釈の方法は子供の頃よくやっていて、月は満ちてくるにしたがって重くなるから、少しずつ月の出が遅くなるんだと思っていたり、地球儀を回しながら、南極はあまり動かないから寒いんだなと妙に納得してみたり、まあそれなりに合理性がないこともないのですが(笑)、でも、大人になった今、さすがにこれでは済まされません。カラーチャートを作った折でもありますので、色についていろいろ考えてみました。
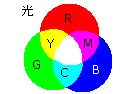
RGBは Red Green Blue の光の三原色、CMYは Cyan Magenta Yellow で、絵具の三原色です。
パソコンではRGBそれぞれを256通り(8bit)の強さで表して、256×256×256=16,777,216 通りの色を表現することが出来ます。これは2の24乗ということで24ビットカラーと呼ばれることがあります。
ここでは、各1ビット ( all or nothing ) にして、3ビット(2の3乗=8色)で表してみます。
各々は、青 + 緑 = シアン (001+010=011)、青 + 赤 = マジェンタ (001+100=101)、赤 + 緑 = 黄色 (100+010=110) などのように足し算をすることができます。このようにRGB3色のうちの2色を足し合わせたものがCMYという関係になっています。3色を全部足すと白(111)になり、全てが無であれば黒(000)です。ここまではすんなり分るのですが、それでは、シアン + マジェンタ (011+101) や、黄色 + 黄色 (110+110) はどうなるんでしょうか。
おとなの方は途中を飛ばして、解決篇からお読みください。→ 解決篇
もし、011+101=110、110+110=000 のようにになってくれれば、光の色と絵具の色の白黒問題は解決に向かいます。これは「排他的論理和」による計算です。
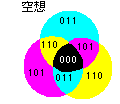 そうはいきませんでした。水色+紫=黄色、黄色+黄色=黒などとはまた突拍子もないことを考えるものです。その突拍子もない空想を図にしてみました。図にして呆れました。こんなことが現実にある訳がないです。未知の関係を解き明かしたような気持に一瞬なったのですが、そうではなかったみたいです。
そうはいきませんでした。水色+紫=黄色、黄色+黄色=黒などとはまた突拍子もないことを考えるものです。その突拍子もない空想を図にしてみました。図にして呆れました。こんなことが現実にある訳がないです。未知の関係を解き明かしたような気持に一瞬なったのですが、そうではなかったみたいです。
色の足し算は「論理和」で計算すべきでした。
赤+緑=黄色を例に、この論理和を模式図にするとこんな感じです。 黄色い光線を輪切りにした図と思ってください。
黄色い光線を輪切りにした図と思ってください。
CMYを論理和で計算すると、水色+紫=白(011+101=111)、黄色+黄色=黄色(110+110=110)です。ふむ、どうなんでしょう。
 ところで、RとC (100 & 011)、GとM (010 & 101)、BとY (001 & 110)のように並べてみて、うまい具合に凹凸関係になっていることに気がつきました。
ところで、RとC (100 & 011)、GとM (010 & 101)、BとY (001 & 110)のように並べてみて、うまい具合に凹凸関係になっていることに気がつきました。
お互いに埋めあえば白(111)になる関係、一方を眺めた後に目をつぶるともう一方の色が見えてくる、補色の関係です。
RGBは Red Green Blue の光の三原色、CMYは Cyan Magenta Yellow で、絵具の三原色です。
パソコンではRGBそれぞれを256通り(8bit)の強さで表して、256×256×256=16,777,216 通りの色を表現することが出来ます。これは2の24乗ということで24ビットカラーと呼ばれることがあります。
ここでは、各1ビット ( all or nothing ) にして、3ビット(2の3乗=8色)で表してみます。
| ... | ..B | .G. | .GB | R.. | R.B | RG. | RGB |
| 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| Black | Blue | Green | Cyan | Red | Magenta | Yellow | White |
各々は、青 + 緑 = シアン (001+010=011)、青 + 赤 = マジェンタ (001+100=101)、赤 + 緑 = 黄色 (100+010=110) などのように足し算をすることができます。このようにRGB3色のうちの2色を足し合わせたものがCMYという関係になっています。3色を全部足すと白(111)になり、全てが無であれば黒(000)です。ここまではすんなり分るのですが、それでは、シアン + マジェンタ (011+101) や、黄色 + 黄色 (110+110) はどうなるんでしょうか。
おとなの方は途中を飛ばして、解決篇からお読みください。→ 解決篇
もし、011+101=110、110+110=000 のようにになってくれれば、光の色と絵具の色の白黒問題は解決に向かいます。これは「排他的論理和」による計算です。
 そうはいきませんでした。水色+紫=黄色、黄色+黄色=黒などとはまた突拍子もないことを考えるものです。その突拍子もない空想を図にしてみました。図にして呆れました。こんなことが現実にある訳がないです。未知の関係を解き明かしたような気持に一瞬なったのですが、そうではなかったみたいです。
そうはいきませんでした。水色+紫=黄色、黄色+黄色=黒などとはまた突拍子もないことを考えるものです。その突拍子もない空想を図にしてみました。図にして呆れました。こんなことが現実にある訳がないです。未知の関係を解き明かしたような気持に一瞬なったのですが、そうではなかったみたいです。色の足し算は「論理和」で計算すべきでした。
赤+緑=黄色を例に、この論理和を模式図にするとこんな感じです。
 黄色い光線を輪切りにした図と思ってください。
黄色い光線を輪切りにした図と思ってください。CMYを論理和で計算すると、水色+紫=白(011+101=111)、黄色+黄色=黄色(110+110=110)です。ふむ、どうなんでしょう。
 ところで、RとC (100 & 011)、GとM (010 & 101)、BとY (001 & 110)のように並べてみて、うまい具合に凹凸関係になっていることに気がつきました。
ところで、RとC (100 & 011)、GとM (010 & 101)、BとY (001 & 110)のように並べてみて、うまい具合に凹凸関係になっていることに気がつきました。お互いに埋めあえば白(111)になる関係、一方を眺めた後に目をつぶるともう一方の色が見えてくる、補色の関係です。
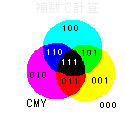
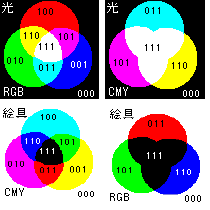 もういちど図を作ってみました。こんどは間違っていないはずです。
光の色は「白い」スクリーンに投影されたときの色であり、絵具の色は「白光」に照らされたときの色、と言うことになります。
もういちど図を作ってみました。こんどは間違っていないはずです。
光の色は「白い」スクリーンに投影されたときの色であり、絵具の色は「白光」に照らされたときの色、と言うことになります。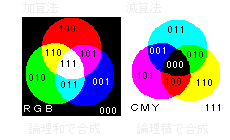
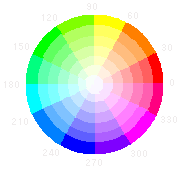
 この両端の赤と赤を繋ぎ合わせれば円盤になるんだろうとは思っていたのですが、なるほど、繋いでみて納得です。色相円環だったんですね。むかし美術の教科書でこんな図を見たことがあります。円の中心を通って向かい合う色は互いに補色の関係でした。Hが色相、Sは彩度、Vは明度です。
この両端の赤と赤を繋ぎ合わせれば円盤になるんだろうとは思っていたのですが、なるほど、繋いでみて納得です。色相円環だったんですね。むかし美術の教科書でこんな図を見たことがあります。円の中心を通って向かい合う色は互いに補色の関係でした。Hが色相、Sは彩度、Vは明度です。